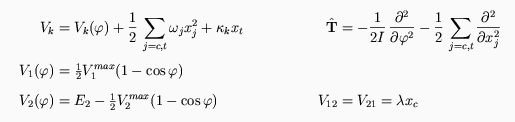
Seite 7: Konische Durchschneidung
>
Auf dieser Seite soll nun die Wellenpaketdynamik für eine konische Durchschneidung studiert werden.
Für eine konische Durchschneidung ist neben der Torsionskoordinate mindestens eine weitere Mode notwendig,
welche die obere mit der unteren elektronischen Fläche koppelt. Diese Art von Mode wird als coupling
mode bezeichnet. Weiterhin gibt es noch die tuning mode, die die Energiedifferenz zwischen den beiden
elektronischen Zuständen varriert (sogenanntes "tuning"). Diese beiden zusätzlichen Moden sind harmonische
Freiheitsgrade, die bestimmte Schwingungen des Moleküls repräsentieren, welche für den
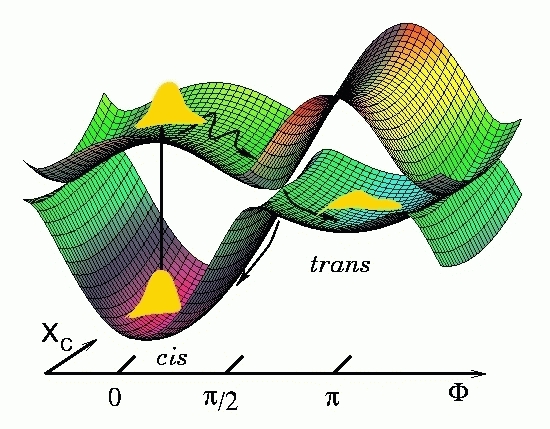
Isomerisierungsprozeß von Bedeutung sind. Wie man sich das Zusammenspiel von Torsionsfreiheitsgrad und der
Kopplungsmode vorzustellen hat, sollen die beiden folgenden Bilder veranschaulichen:
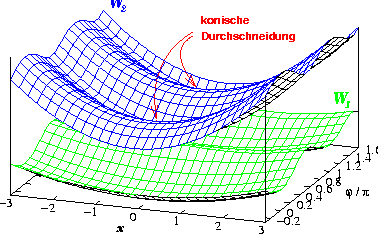
Adiabatische Darstellung
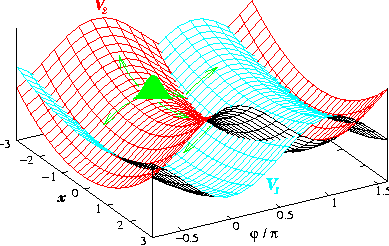
| Diabatische Darstellung
|
| 
|
In der adiabatischen Darstellung ist der photochemische Trichter sehr gut zu erkennen. Dieser bewirkt eine effiziente
Lokalisierung des Wellenpakets am Ort der Kopplung zwischen den beiden elektronischen Flächen. In der diabatischen
Darstellung sind die Bewegungsmöglichkeiten des auf der oberen Fläche initiierten Wellenpakets angedeutet und
sollen weiter unten durch eine animierte 3D-Graphik lebendig werden. Doch zuvor noch ein kurzer Blick auf die Terme des
Hamiltonoperators:
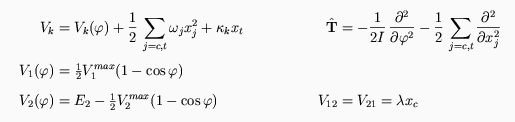
Die potentielle Energie beinhaltet wie zuvor auch die beiden elektronischen Torsionspotentiale, wird diesmal aber erweitert
um die potentielle Energie der harmonischen Moden xc und xt , wobei c
für die Kopplungsmode und t für die Tuningmode steht. Der Potentialgradient  an der Stelle
an der Stelle 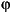 =0 gibt an, wie stark entlang der Tuning-Mode die obere elektronische Fläche
gegenüber der unteren verschoben ist und damit den Energieabstand zwischen diesen beiden Flächen verringert.
Natürlich haben die beiden harmonischen Moden auch einen Beitrag in der kinetischen Energie. Dem Kopplungsterm
V12 ist die lineare Abhängigkeit von der Kopplungsmode zu entnehmen und
=0 gibt an, wie stark entlang der Tuning-Mode die obere elektronische Fläche
gegenüber der unteren verschoben ist und damit den Energieabstand zwischen diesen beiden Flächen verringert.
Natürlich haben die beiden harmonischen Moden auch einen Beitrag in der kinetischen Energie. Dem Kopplungsterm
V12 ist die lineare Abhängigkeit von der Kopplungsmode zu entnehmen und  ist die Kopplungskonstante.
ist die Kopplungskonstante.
Auf der nächsten Seite können die animierten Wellenpaketsbewegungen betrachtet werden!